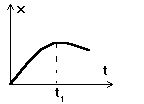Я физик и имею право на сохранение энергии

Прочитать и решить в конце задачи.

Условие.

Зависимость скорости от времени для материальной точки имеет вид v = 2 + 6t. Написать уравнение для координаты, если в начальный момент времени тело находилось в точке с координатой -5 (все величины даны в системе СИ). Найти ускорение тела, путь и перемещение, пройденные им за 10 с.

Решение.

Какие ключевые понятия помогают нам выделить признаки, по которым мы определим характер движения тела? Прежде всего, это “скорость”, “координата”, “ускорение”, “путь”, “перемещение” - они в явном виде присутствуют в условии. Координат у тела может быть три (x, y, z), две (x, y) или одна (x). Раз нам сказано “найти координату” (а не координаты), то значит мы имеем дело с движением вдоль одной прямой (единственное число - одна координата - одна прямая). Итак, движение прямолинейное. Скорость - меняется или не меняется в процессе движения? Ответить на этот вопрос нам поможет уравнение для скорости. Из него мы видим, что в РАЗНЫЕ моменты времени t значения скорости v тоже РАЗНЫЕ. Значит, скорость меняется, значит движение не является равномерны, т.е. скорее всего одно равноускоренное. Для того, чтобы принять окончательное решение о характере движения тела, нужно вспомнить что-либо о свойствах равноускоренного движения и сравнить с нашей ситуацией. Вспоминаем. Ага, вспомнили: при равноускоренном движении справедливы два уравнения (одно для скорости, другое для перемещения), которые имеют вид: v = v₀ + a D t, D S = v₀ D t + a D t² /2. В нашей задаче тоже есть уравнение для скорости. Давайте сравним наше уравнение и общее, напишем их рядышком друг с другом и внимательно посмотрим на них:

v = v₀ + a D t,

v = 2 + 6t.

Что мы должны обнаружить при СРАВНЕНИИ этих формул? Во-первых, чем они отличаются, а во-вторых, что в них одинакового. Главный вопрос, на который мы должны ответить, можно ли ПРОСТОЙ ПОДСТАНОВКОЙ превратить одну формулу в другую?

Первое, что нужно сказать, что раз в задаче нет различных участков движения, то все времена измеряются от начального времени t₀ = 0 и тогда D t = t - t₀ = t. Значит, отличие формул еще меньше, чем кажется на первый взгляд:

v = v₀ + at,

v = 2 + 6t.

Теперь ясно видно, что если вместо v₀ подставить 2, в вместо а подставить 6, то мы из первой формулы сразу получим вторую! Вывод, наша КОНКРЕТНАЯ формула для скорости является ЧАСТНЫМ случаем ОБЩЕЙ формулы для скорости равноускоренного движения. Следовательно, наше тело совершает равноускоренное движение. Причем, мы сразу можем сказать КОНКРЕТНЫЕ значения начальной скорости и ускорения нашего тела: v₀ =2 м/с, а = 6 м/с².

Теперь легко написать остальные конкретные уравнения для движения нашего тела. Чтобы их получить, нужно в общие уравнения равноускоренного движения подставить конкретные значения рассматриваемой частной ситуации. Значит, мы берем уравнение для перемещения D S = v₀ D t + a D t² /2 и вместо D t пишем t, вместо v₀ пишем 2, вместо а пишем 6. Получаем D S = 2 t + 6 t² /2 = 2t + 3 t². Наша задача - написать уравнение для координаты. Перемещение и координаты связаны, ведь если тело перемещается, то его координаты меняются. Как связаны эти величины? Смотрим в наш список; при прямолинейном движении D S = х - х_о, откуда х = х_о + D S. По условию начальная координата х_о = -5, тогда уравнение для координаты принимает вид х = -5 + 2t + 3 t². Осталось найти путь и перемещение. Перемещение находится простым вычислением значения D S = 2t + 3 t² при t = 10: т.е. D S = 2· 10 + 3· 10² = 320 м. Так при своем движении тело двигалось все время в одном направлении (координата только увеличивалась, точек поворота не было и тело назад не возвращалось), то путь будет совпадать с перемещением: S = D S = = 320 м.

Задача № 26.

Условие.

Уравнение движения материальной точки имеет вид x = 2t - 0,2 t² . Написать уравнение для скорости движения тела, найти ускорение, скорость, путь и перемещение через 8 секунд после начала движения.

Решение.

Для того, чтобы определить характер движения тела, мы в этой задаче имеем только уравнение для его координаты. Значит, мы должны сравнить это уравнение со всеми общими уравнениями движения, которые мы знаем. Нам известны пока лишь два типа движения: равномерное и прямолинейное равноускоренное. Для равномерного движения уравнение координаты имеет вид (это мы находим в списке основных кинематических величин) x = x₀ + v D t, но поскольку участок движения у нас в этой задаче один и время отсчитывается от нуля, то D t = t и окончательно x = x₀+ v t. Для равноускоренного движения уравнение выглядит следующим образом (смотрите предыдущую задачу, кроме того сразу учитываем, что D t = t) x = x_o + v_o t + a t² /2.

Радикальное отличие этих двух уравнений: x = x₀ + v t и x = x_o + v_o t + a t² /2 заключается в том, что первое уравнение содержит t в первой степени, а второе во второй (t²). Главный отличительный признак - есть или нет в уравнении для координаты квадрат времени: если нет - движение равномерное; если есть - движение равноускоренное! Теперь внимательно глядим на наше конкретное уравнение нашей конкретной задачи. Есть квадрат? Есть! Вывод? Наше тело движется равноускоренно. А так как положение тела описывается только одной координатой, то это движение прямолинейное (вдоль оси координат х).

Прямолинейное равноускоренное движение описывается еще и уравнением для скорости v = v_o + at. Чтобы это уравнение записать конкретно для нашей задачи, нужно знать конкретные значения для начальной скорости v_o и ускорения а. Откуда мы их возьмем? У нас есть возможность сравнить ОБЩЕЕ и КОНКРЕТНОЕ уравнения для координаты:

x = x_o + v_o t + a t² /2

x = 2t - 0,2 t² .

И то и другое уравнения описывают равноускоренное прямолинейное движение. Просто, первое записано в общем виде (без конкретных чисел), а второе уже с конкретными числами. Чтобы из общего уравнения получить конкретное, нужно вместо букв подставить числа. Спрашивается, вместо каких букв и какие числа нужно подставить в общее уравнение, чтобы из него получилось наше конкретное. Это тест на внимательность. Кто его прошел, тот заметил, что если вместо x_o подставить 0 (если величины нет, значит ее значение ноль!), вместо v_o подставить 2, вместо a/2 (вот где особая хитрость) подставить - 0,2 (не теряйте знак!), то получим сразу наше конкретное уравнение. Тогда мы можем сделать вывод, что для нашей конкретной задачи имеем: x_o = 0, v_o = 2, a/2 = - 0,2! Начальная координата равна нулю, т.е. тело в начальный момент времени тело находилось в начале координат. Начальная скорость равна 2 м/с. Половина (!) ускорения равна 0,2 м/с², значит само ускорение равно а = - 0,4 м/с². Теперь нам известны все параметры, необходимые для ПОЛНОГО описания равноускоренного прямолинейного движения. Уравнение для скорости принимает вид v = 2 - 0,4t. Итак, для нашего случая уравнения имеют вид: x = 2t - 0,2 t² , v = 2 - 0,4t. Зная уравнения движения можно найти ВСЕ, что только понадобиться узнать об этом движении.

Через 8 с после начала движения, т.е. при t = 8, координата и скорость будут равны: x = 2· 8 - 0,2· 8² = 3,2 м, v = 2 - 0,4· 8 = -1,2 м/с. Перемещение при прямолинейном движении всегда находится как D S = х - х_о = 3,2 - 0 = 3,2 м. Осталось найти путь. Если в процессе движения тело движется все время в одном направлении, то путь совпадает с перемещением. Значит, первое, что мы должны определить, поворачивало ли тело назад или нет в течение нужных нам восьми секунд? Для этого есть несколько способов, но самый универсальный - построить график зависимости координаты от времени и на нем сразу все будет видно. График зависимости координаты от времени при равноускоренном движении имеет вид параболы.

В нашем случае эта парабола описывается уравнением вида x = 2t - 0,2 t². При квадратичном члене уравнения стоит ОТРИЦАТЕЛЬНЫЙ коэффициент (-0,2), что говорит о том, что ветви параболы идут ВНИЗ!

Достаточно нарисовать этот график только схематично, чтобы увидеть наличие точки поворота: до момента времени t₁ координата тела увеличивалась, а после этого момента времени стала уменьшаться. Это и означает, что тело повернуло в обратную сторону. Если время t₁ больше восьми секунд (если t₁ > 8), то наше тело до восьми секунд двигалось без поворота. Чтобы сравнить t₁ со значением 8, нужно просто найти это t₁. Но как это сделать? Мы уже раньше говорили о том, что там где у параболы вершина, там скорость равна нулю. Действительно, тело, прежде чем повернуть в обратную сторону, должно на мгновение остановиться. Значит, при t = t₁ должно быть v = 0. Иначе говоря, если в уравнение для скорости вместо t подставить t₁, то вместо v мы одновременно должны подставить 0. Давайте сделаем это, тогда получим, что 0 = 2 - 0,4 t₁. Отсюда находим время точки поворота t₁ = 2/0,4 = 5 с. Очевидно, 5 < 8. Значит наше тело двигалось 5 секунд вдоль оси координат (значения координат увеличивались), а следующие 3 секунды оно двигалось обратно (значения координат уменьшаются). Это говорит нам о том, что в данной ситуации путь и перемещение не равны друг другу. Тело сначала удалилось, а потом вернулось немного обратно, значит переместилось не очень далеко, путь же, пройденный телом, будет увеличиваться постоянно, т.е. путь будет теперь больше перемещения (интересно, а может путь быть меньше перемещения?). Раз есть точка поворота, значит движение тела можно разбить на два участка: на первом участке координата увеличивалась, а на втором - уменьшалась. Весь путь, пройденный телом, складывается из путей, пройденных на каждом отдельном участке. Будем знать эти отдельные пути - сможем найти и общий (простым сложением).

Первый участок движения занял 5 секунд. В конце этого участка координата стала равна x = 2· 5 - 0,2· 5² = 5 м. Значит за первые 5 с тело прошло 5 м вдоль оси координат. За оставшиеся 3 с тело вернулось обратно, дойдя до конечной точки с координатой 3,2 м (которую мы уже сосчитали выше). Двигаясь против оси координат от точки 5 до точки 3,2, тело прошло путь 5 - 3,2 = 1,8 м. Следовательно, полный путь, пройденный телом, составляет 5 + 1,8 = 6,8 м.

В нашем случае у нас был еще один признак, говорящий о том, что у тела была точка поворота - это отрицательное значение скорости (-1,2 м/с). Знак “-” как раз и говорит о том, что скорость стала направлена в противоположном направлении (была 2, стала -1,2 - поменялся знак, поменялось направление). Однако, установив этот факт по знаку скорости, мы все равно в дальнейшем были бы вынуждены найти время точки поворота, разбить все движение на участки, найти путь на каждом участке и потом вычислить общий путь. То есть, мы все равно проделали бы все те же самые вычисления.

Первый уровень

1. Автомобиль начинает движение с ускорением 0,5 м\с2. Определите скорость и путь автомобиля за первые 2 секунды движения.
2. Материальная точка движется по закону х = 2 + 2t – t2 Определите начальную координату, начальную скорость и ускорение точки. Запишите уравнение скорости и постройте график.
3. В момент начала наблюдения расстояние между двумя телами было равно 6 м. Первое тело движется из состояния покоя с ускорением 2 м/с3. Второе движется вслед за ним, имея начальную скорость 2 м/с и ускорение 4 м/с2. Написать уравнения x(t) и найти место и время встречи тел.
4. Катер, трогаясь с места, за 5 секунд набирает скорость 54 км\ч. С каким ускорением движется катер и чему равно его перемещение за это время?

Второй уровень

5. Тормозная система автомобиля обеспечивает торможение с максимальным ускорением -6м\с2. Определите, какое время потребуется автомобилю, движущемуся со скоростью 72 км\ч, для экстренной остановки и определите тормозной путь автомобиля.
6. В результате торможения скорость автомобиля за 3 секунды уменьшилась с 72 км /ч до 7,2 км\ч. Определите ускорение автомобиля.
7. Материальная точка движется по закону х = 4t + 2t2 .Определите начальную координату, начальную скорость и ускорение точки. Запишите уравнение скорости и постройте график.
8. Движение двух мотоциклистов заданы уравнениями x1=15+t2, X2=8t. Описать движение каждого мотоциклиста; найти место и время встречи.
9. За 10 секунд до финиша скорость велосипедиста равнялась 36 км\ч. а на финише - 72 км\ч. С каким ускорением финишировал велосипедист.
10. Тело, начавшее двигаться равноускорено из состояния покоя, за 4 секунды проходит путь 80 м. С каким ускорением двигается тело?
11. Велосипед съехал с горки за 5с,двигаясь с постоянным ускорением 0.5м/с.Определите длину горки,если известно,что в начале спуска скорость велосипедиста была равна 18км/ч.